peu d'intérêt pour la radio.
Rappel:
sur la terre une minute d'arc de grand cercle vaut un mille nautique ( Nm ), un degré vaut soixante minutes et
un Nm vaut 1852 mètres.
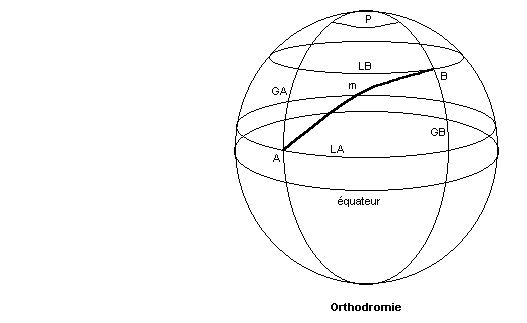
L'orthodromie:
Il existe une infinité de routes entre deux points. Il en est cependant deux qui présentent un intérêt
particulier pour la navigation. Pour représenter un déplacement, l'outil privilégié est la carte et la
tentation est grande de tracer une ligne droite entre deux points, mais suivant le type de carte utilisé
cette droite correspond à une orthodromie, ou à une loxodromie ou... à n'importe quoi. En effet, la terre
est une sphère et représenter une sphère sur une surface plane revient à résoudre la "quadrature du cercle".
C'est pourquoi il existe un grand nombre de méthodes de projection présidant à la confection des cartes,
suivant l'usage auxquelles elles sont destinées. Les critères importants sont la préservation des angles,
des distances, des surfaces ou la constance de l'échelle. Aucun type de projection ne réunit ces quatre
critères. Bien évidemment, tout ceci n'est critique que pour des grandes distances et les erreurs de distance
ou d'angle sur une carte routière sont tout à fait négligeables.
C'est la route qui fait un angle constant avec tous les méridiens. Elle se mesure sur une carte Mercator, sur
laquelle tous les méridiens sont parallèles entre eux et perpendiculaires aux ...parallèles. Sur cette carte
toutes les droites sont des loxodromies, l'angle de route se mesure directement à l'intersection d'un méridien
avec un rapporteur et la distance se mesure sur un méridien proche à l'aide d'un compas. L'échelle évolue avec
la latitude et la mesure de distance doit se faire le long du méridien autour de la latitude moyenne du trajet.
Cette route est surtout utilisée pour des courtes distances (1000 Nautical Miles) aux latitudes basses et
moyennes.
C'est la route la plus courte sur la sphère entre deux points situés sur cette sphère. Il ne s'agit pas de la
ligne droite qui serait souterraine, mais bien d'un déplacement en surface. C'est en fait ce qu'on appelle un
arc de grand cercle, unique, passant par ces points. Il a même diamètre et même circonférence que les méridiens
et l'équateur. On suppose ici que la terre est une sphère parfaite. La carte "à peu près" orthodromique, où
l'orthodromie est une droite est la carte Lambert. C'est une projection conique et les droites ne représentent
des orthodromies que dans le voisinage du parallèle de tangence.
Pour ceux qui disposent d'un globe il existe un moyen simple de matérialiser l'orthodromie; il suffit de tendre
un fil, sur le globe, entre les deux points. Ce procédé permet de se rendre compte de l'évolution de l'angle
de route et de régions survolées.
Les ondes radios étant plutôt futées, elles ont décidé d'emprunter le chemin le plus court et donc de suivre
l'orthodromie.
Pour les OM's il existe la carte azimutale où l'orthodromie est une droite entre le point central fixe pour
lequel la carte a été construite et tous les autres points de la carte. Sur cette carte les méridiens ou
l'équateur, qui sont des grands cercles et donc des orthodromies, sont représentées par des courbes, ce qui
prouve bien qu'elle ne peut pas être considérée comme orthodromique sur toute son étendue. L'usage en est donc
limité en un seul lieu.
Je passe sous silence les formules de la loxo. Elles sont aussi gratinées que celles de l'ortho et présentent
peu d'intérêt pour la radio.
Rappel:
sur la terre une minute d'arc de grand cercle vaut un mille nautique ( Nm ), un degré vaut soixante minutes et
un Nm vaut 1852 mètres.

L'orthodromie:
soit LA latitude de A LB latitude de B
GA longitude de A GB longitude de B
P pôle nord ou sud
On code: latitude nord positif
latitude sud négatif
longitude ouest positif
longitude est négatif
Dans la suite du texte * = multiplication / = division
calcul préliminaire: P (angle au pôle ) = GB - GA
dL (diff de lat. ) = LB - LA
On fait appel à la trigonométrie sphérique pour résoudre le triangle sphérique APB.
Distance orthodromique m:
cos m = sin LA * sin LB + cos LA * cos LB * cos P
et
m = Arc cos(sin LA..... cos P)
ou
cos m = (cos P -1) * cos LA * cos LB + cos dL
m est un angle, par exemple en degré, que l'on converti en distance (voir rappel).
m en degré décimaux * 60 = distance en Nm
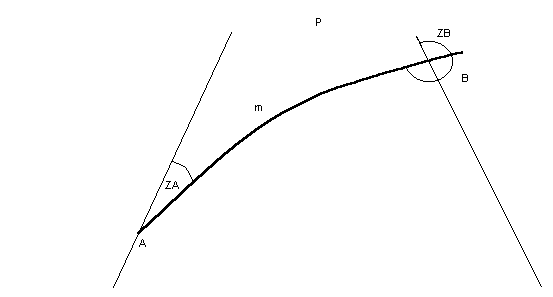
Azimut en A ou route ortho de A vers B ZA: sin ZA = cos LB * sin P / sin m (1) cette formule tirée de l'analogie des sinus n'est pas pratique car elle ne délivre que des angles compris entre -90 ° et 90 °: on est alors obligé de faire un schéma de lever de doute ou au moins 2 tests, un sur le signe de P et un sur le signe de dL pour déterminer la route exacte de 0 à 360 °. on lui préfère donc: cos ZA = sin LB / ( sin m * cos La ) - tg LA / tg m (2) si P est négatif (chemin est ) route = ZA si P est positif (chemin ouest) route = 360 - ZA Azimut en B ou route ortho de B vers A ZB: dans (1) P devient -P et on remplace A par B et B par A. dans (2) idem, P n'intervenant que pour le test. dans (2) si on ne change pas le signe de P pour le test on obtient la route d'arrivée en B c.à.d ZB + 180.
Ceux qui consulteront "Mathématiques de l'Ingénieur" chez Dunod pour vérifier les formules de trigonométrie
sphérique, page 50, auront l'impression que j'ai fait une salade entre les sinus et les cosinus. Qu'ils se
rassurent en considérant que dans le triangle APB l'arc AP, par exemple, est la colatitude de A (90 - LA)
et que tout rentre dans l'ordre puisque sin(90 - LA) = cos LA et cos(90-LA)= sin LA.
Les formules sont disponibles dans le classeur Excel Omctrlw.xls sous l'onglet "Z ligne ortho" disponible ici:
Feuilles de calculs sous Excel
Il y a bien longtemps que le basic est n'est plus utilisé en programmation. Ce listing a pour but d'illustrer
la technique pour les conversions angulaires et l'ordre des calculs. Et qui sait? Un copier-coller dans une
fenêtre Dos...
10 CLS:PRINT "Programme Orthodromie OM de A vers B":PRINT
20 PI=4*ATN(1):DR=180/PI:US$="#####.##":D=360
30 DEF FNRM(X)=(SGN(X)*(INT(ABS(X))+((ABS(X)-INT(ABS(X)))/.6)))/DR
40 REM DEG.MIN -> RADIAN
50 DEF FNASN(X)=ATN(X/SQR(-X*X+1)):REM ARC SINUS
60 DEF FNACS(X)=PI/2-FNASN(X):REM ARC COSINUS
70 INPUT "LAT A:",LA:LAR=FNRM(LA):INPUT"LONG A:",GA:GAR=FNRM(GA)
80 INPUT "LAT B:",LB:LBR=FNRM(LB):INPUT"LONG B:",GB:GBR=FNRM(GB)
90 P=GBR-GAR:P=FNACS(COS(P))*SGN(SIN(P))
100 M=SIN(LAR)*SIN(LBR)+COS(LAR)*COS(LBR)*COS(P):M=FNACS(M)
110 MNM=M*DR*60:PRINT "DISTANCE",
120 PRINT USING US$;MNM;:PRINT " Nm",
130 PRINT USING US$;MNM*1.852;:PRINT " Km"
140 Z=SIN(LBR)/SIN(M)/COS(LAR)-TAN(LAR)/TAN(M):ZAR=DR*FNACS(Z)
150 Z=SIN(LAR)/SIN(M)/COS(LBR)-TAN(LBR)/TAN(M):ZBR=DR*FNACS(Z)
160 SA=0:IF P>0 THEN SA=D
170 SB=ABS(SA-D):ZA=ABS(SA-ZAR):ZB=ABS(SB-ZBR)
180 PRINT "AZIMUT DE A -> B";:PRINT USING US$;ZA;:PRINT " ø"
190 PRINT "AZIMUT DE B -> A";:PRINT USING US$;ZB;:PRINT " ø"
200 END:REM (c) Jean Burgard
Page d'accueil